Accueil

 Renaud

 Environnement

 Bandes dessinées

Mathématiques 

Jeux

 Liens

 Accueil<Mathématiques<La démonstration en 5ème
L'espace mathématiques de ChezJeff :
Les activités 6ème - 5ème - 4ème - 3ème - Les quadrilatères
Une aire variable - Le projet polyèdre - Les théorèmes inédits -
Les énigmes géométriques - Les énigmes du professeur Ninja
La démonstration en 4ème - en 5ème - Forum -- Bibliographie

 APPRENDRE A REDIGER UNE DEMONSTRATION (en 5ème)
Allez aux exercices

 En Mathématiques, observer, prendre des mesures … ne suffisent pas à prouver qu'un énoncé est vrai.
Il faut utiliser un raisonnement.
 Un raisonnement peut se décomposer en trois étapes :
 J'analyse les données du problème : elles sont connues soit par l'énoncé du problème, soit par l'intermédiaire d'un raisonnement précédent ou d'une réponse à une question précédente. Je choisis celles qui vont me permettre d'utiliser une définition, une propriété ou un théorème.
 J'utilise la définition, la propriété ou le théorème adapté vus en cours. Attention, je ne les choisis pas au hasard, j'écris ceux qui permettent de répondre à la question posée.
 J'écris la conclusion, c'est à dire ce je peux dire grâce à la propriété (souvent ce que l'on veut démontrer).
REDACTION : Je rédige de la manière suivante :
On a j'écris les données
Or, on sait que j'écris la définition ou la propriété ou le théorème
Donc j'écris la conclusion
PROPRIETES ET THEOREMES :
On utilise souvent des propriétés ou des théorèmes de la forme :
Si ……………........, alors ………........................……
 Par exemple :

 Si un quadrilatère a ses diagonales qui se coupent en leur milieu,   alors c'est un parallélogramme.

 
Condition (après "Si")

 
Conclusion (après "alors")

 Lorsqu'on inverse la condition et la conclusion d'une propriété, on obtient la propriété réciproque :

 Si un quadrilatère est un parallélogramme  alors ses diagonales se coupent en leur milieu.

 
Condition

 
Conclusion


 Attention, la réciproque d'une propriété vraie n'est pas forcément vraie, par exemple :
Propriété vraie : Si un nombre se divise par 4 alors il a se divise par 2.
Réciproque fausse : Si un nombre se divise par 2 alors il se divise par 4
 

 
FAUX, 6 se divise par 2, mais pas par 4 !

EXEMPLE DE DEMONSTRATION :
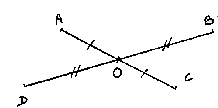
Enoncé de l'exercice : Je considère la figure ci-contre.
Quelle est la nature du quadrilatère ABCD?

Je réfléchis : On me demande trouver la nature du quadrilatère ABCD. Je le trace et il semble que se soit un parallélogramme. Avec la figure donnée, il semble aussi que je dois travailler à partir des diagonales. Je cherche si je connais une propriété sur les diagonales d'un quadrilatère, dont la conclusion indique que c'est un parallélogramme. Puis je vérifie si cette propriété peut être appliquée à cet exercice.

  

 Je rédige :
On a O milieu de [AC] et [DB] les diagonales de ABCD.

Or, on sait que si un quadrilatère a ses diagonales qui se coupent en leur milieu, alors c'est un parallélogramme.

Donc ABCD est un parallélogramme.


 APPLICATION SOUS LA FORME D' EXERCICES
Exercice 1 - Exercice 2 - Exercice 3

 Exercice 1 : compléter les démonstrations à trous qui suivent
On a (AB) (GH) et (IJ) (GH)
Or on sait que si deux droites sont perpendiculaires à la même droite alors elles sont parallèles entre elles
Donc .......................................		 On a ABC triangle isocèle en A
Or on sait que .................……
.....................................................
Donc AB = AC		 On a ……......................................
Or on sait que la médiatrice d'un segment est la droite perpendiculaire à ce segment en son milieu
Donc (AB) passe par le milieu de [IJ]

On a EFGH parallélogramme
Or on sait qu'un parallélogramme a ses côtés opposés de même longueur.
Donc ……………………………		 On a (AB)//(IJ) et (EF)//(IJ)
Or on sait que ….........................
.......................................................
......................................................
Donc (AB)//(EF)		 On a ………..........................................
Or on sait que si un quadrilatère a ses côtés opposés parallèles, alors c'est un parallélogramme
Donc ABCD parallélogramme

Exercice 2 :
Cliquer à chaque fois sur les bonnes données, la bonne propriété et la bonne conclusion qui vont permettre de résoudre cet exercice

Enoncé : On considère la figure ci-contre. O est le centre des deux cercles de diamètres [AC] et [BD]
1- Démontrer que ABCD est un parallélogramme
2- En déduire que (AD) est parallèle à (BC)		  Figure :

 Réponse à la question 1 :
On a :
O milieu de [AC] et [BD] diagonales de ABCD

 
On a :
[AC] et [BD] diamètres et diagonales de ABCD

 
On a : [AC] et [BD]diamètres d'un cercle de centre O donc O milieu de [AC] et [BD] diagonales de ABCD

 
Or on sait que si ABCD est un parallélogramme alors ses diagonales se coupent en leur milieu

 
Or on sait que les diagonales d'un quadrilatère se soupent en leur milieu alors c'est un parallélogramme

 
Or on sait que deux diamètres forment un parallélogramme


 
Donc ABCD parallélogramme

 
Donc O milieu des diagonales

 
Donc [AC] et [BD] diamètres .

 


 Réponse à la question 2:
On a (AD) est parallèle à (BC)

 
O milieu de [AC] et [BD] diagonales de ABCD

 
On a ABCD parallélogramme

 
Or on sait que si les côtés opposés d'un quadrilatère sont parallèles alors c'est un parallélogramme

 
Or on sait dans un parallélogramme, les côtés opposes ont la même longueur

 
Or on sait dans un parallélogramme, les côtés opposes sont parallèles

 
Donc ABCD parallélogramme

 
Donc (AD) est parallèle à (BC)

 
Donc (CD) est parallèle à (BA)

 


Exercice 3 :
Exercice à rédiger seul.
Remarque : les angles ne sont pas notés correctement (il manque le "chapeau")
IJKL est un parallélogramme avec IJK = 70° et IJ = 8 cm.
Tracer la bissectrice de l'angle LIJ, elle coupe le côté [KL] en H.
Démontrer que JIH = 55°