Accueil

 Renaud

 Environnement

 Bandes dessinées

Mathématiques 

Jeux

 Liens

Accueil<Mathématiques<La démonstration en 4ème
L'espace mathématiques de ChezJeff :
Les activités 6ème - 5ème - 4ème - 3ème - Les quadrilatères
Une aire variable - Le projet polyèdre - Les théorèmes inédits -
Les énigmes géométriques - Les énigmes du professeur Ninja
La démonstration en 4ème - en 5ème - Forum -- Bibliographie

 APPRENDRE A REDIGER UNE DEMONSTRATION (en 4ème)
 Allez aux exercices

 En Mathématiques, observer, prendre des mesures … ne suffisent pas à prouver qu'un énoncé est vrai.
Il faut utiliser un raisonnement.
 Un raisonnement peut se décomposer en trois étapes :
J'analyse les données, et je choisis celles qui sont nécessaires pour qu'une définition, une propriété ou un théorème soit utilisable. Elles doivent être connues soit par l'énoncé du problème, soit par l'intermédiaire d'un raisonnement précédent ou d'une réponse à une question précédente.
J'utilise la définition, la propriété ou le théorème adapté vus en cours.
J'écris la conclusion, c'est à dire ce qui est déduit grâce à la propriété (souvent ce que l'on veut démontrer).
 On utilise souvent des propriétés de la forme : Si …………….., alors …………………
 Par exemple :

 Si un point est sur la médiatrice d'un segment,   alors il est équidistant des extrémités de ce segment

 
Condition

 
Conclusion

 Lorsqu'on inverse la condition et la conclusion d'une propriété, on obtient la propriété réciproque :

 Si un point est équidistant des extrémités d'un segment   alors il est sur la médiatrice de ce segment.

 
Condition

 
Conclusion


 Attention, la réciproque d'une propriété vraie n'est pas forcément vraie, par exemple :
Propriété vraie : Si un quadrilatère est un carré alors il a 4 côtés de même longueur.
Réciproque fausse : Si un quadrilatère a 4 côtés de même longueur alors c'est un carré
 

 
FAUX, c'est un losange !

Exemple de démonstration :
Enoncé de l'exercice : Soit C un cercle de centre O et de rayon 4 cm. Soient A et B deux points du cercle C. Démontrer que O est un point de la médiatrice de [AB].

Je réfléchis : On me demande de démontrer que O est un point de la médiatrice de [AB]. Je cherche si je connais une propriété dont la conclusion indique qu'un point est sur la médiatrice d'un segment. Puis je vérifie si cette propriété peut être appliquée à cet exercice (c'est à dire que les données de l'exercice doivent vérifier la condition de la propriété).

  

 Je rédige :
On a (ici j'écris les données) OA = OB = rayon du cercle = 4 cm , c'est à dire O est équidistant des points A et B.
Or, on sait que (ici j'écris la propriété) si un point est équidistant des extrémités d'un segment alors il est sur la médiatrice de ce segment.
Donc (ici j'écris la conclusion) O est sur la médiatrice de [AB]


 APPLICATION SOUS LA FORME D'UN EXERCICE


Cliquer à chaque fois sur les bonnes données, la bonne propriété et la bonne conclusion qui vont permettre de résoudre cet exercice

Enoncé : Tracer un triangle ABC rectangle en A. Placer D le symétrique de B par rapport à A. Tracer (d) la médiatrice de [BC], elle coupe (AC) en O.
1- Démontrer que (AC) est la médiatrice de [BD].
2- Démontrer que O est le centre du cercle circonscrit au triangle BDC.		  Figure :

 Réponse à la question 1 :
 On a :
· ABC rectangle en A
· D symétrique de B par rapport à A

 
 On a : · D symétrique de B par rapport à A donc A milieu de [BD]
· (AC) perpendiculaire à (BD) par construction

 
 On a :
· (AC) est la médiatrice de [BD]


 
Or on sait que si un point est équidistant des extrémités d'un segment, alors il est sur la médiatrice de ce segment.

 
Or on sait que si un point est sur la médiatrice d'un segment, alors il est équidistant des extrémités de ce segment.

 
Or on sait que la médiatrice d'un segment est la droite perpendiculaire à ce segment en son milieu

 
Donc A milieu de [BD]

 
Donc (AC) est la médiatrice de [BD]

 
Donc A est sur la médiatrice de [BD]

 


 Réponse à la question 2:
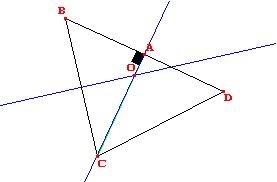
 On a :
· O est le centre du cercle circonscrit au triangle BDC
· (AC) est la médiatrice de [BD]

 
 On a :
· (AC) est la médiatrice de [BD]
· (d) est la médiatrice de [BC]

 
 On a :
· (AC) est la médiatrice de [BD]
· (d) est la médiatrice de [BC]
· O intersection de (d) et (AC)

 
Or on sait que les médiatrices d'un triangle sont concourantes en un point : le centre du cercle circonscrit

 
Or on sait que la médiatrice d'un segment est la droite perpendiculaire à ce segment en son milieu

 
Or on sait que dans un triangle rectangle le centre du cercle circonscrit est le milieu de l'hypoténuse.

 
Donc O est sur la médiatrice de [CD]

 
Donc O est le milieu du triangle

 
Donc O est le centre du cercle circonscrit au triangle BDC